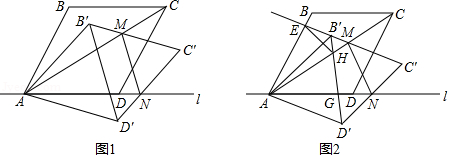
如图1,菱形的顶点,在直线上,,以点为旋转中心将菱形顺时针旋转,得到菱形,交对角线于点,交直线于点,连接.
(1)当时,求的大小.
(2)如图2,对角线交于点,交直线与点,延长交于点,连接.当的周长为2时,求菱形的周长.
相关知识点
推荐套卷
如图1,菱形的顶点,在直线上,,以点为旋转中心将菱形顺时针旋转,得到菱形,交对角线于点,交直线于点,连接.
(1)当时,求的大小.
(2)如图2,对角线交于点,交直线与点,延长交于点,连接.当的周长为2时,求菱形的周长.
