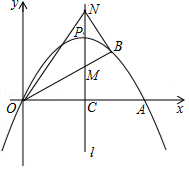
如图,顶点为的二次函数图象与轴交于点,点在该图象上,交其对称轴于点,点、关于点对称,连接、.
(1)求该二次函数的关系式.
(2)若点在对称轴右侧的二次函数图象上运动,请解答下列问题:
①连接,当时,请判断的形状,并求出此时点的坐标.
②求证:.
相关知识点
推荐套卷
如图,顶点为的二次函数图象与轴交于点,点在该图象上,交其对称轴于点,点、关于点对称,连接、.
(1)求该二次函数的关系式.
(2)若点在对称轴右侧的二次函数图象上运动,请解答下列问题:
①连接,当时,请判断的形状,并求出此时点的坐标.
②求证:.
