胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
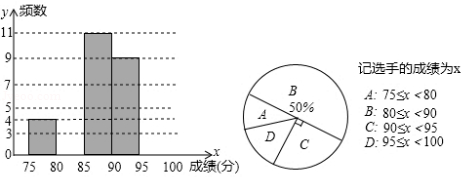
请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形对应的圆心角度数;
(2)成绩在区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
相关知识点
推荐套卷
胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:

请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形对应的圆心角度数;
(2)成绩在区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.