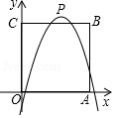
如图，在平面直角坐标系中，正方形的边长为4，边，分别在轴，轴的正半轴上，把正方形的内部及边上，横、纵坐标均为整数的点称为好点．点为抛物线的顶点．
（1）当时，求该抛物线下方（包括边界）的好点个数．
（2）当时，求该抛物线上的好点坐标．
（3）若点在正方形内部，该抛物线下方（包括边界）恰好存在8个好点，求的取值范围．
相关试题
（·辽宁丹东）在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN
90°．
（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系．
（·黑龙江绥化）如图1，在正方形ABCD中，延长BC至M ,使BM="DN" ,连接MN交BD延长线于点E．
（1）求证：BD+2DE=
BM ．
（2）如图2 ，连接BN交AD于点F ，连接MF交BD于点G．若AF:FD="1:2" ,且CM=2，则线段DG=_______．
（·黑龙江绥化）在平面直角坐标系xoy中 ,直线y="-x+3" 与x轴、y轴分别交于A、B ，在△AOB内部作正方形，使正方形的四个顶点都落在该三角形的边上，求正方形落在x轴正半轴的顶点坐标。
推荐套卷
粤公网安备 44130202000953号