某公司投资700万元购买甲、乙两种产品的生产技术和设备后,进行这两种产品的生产加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价定在35元到70元之间较为合理,设甲种产品的销售单价为x(元),年销售量为y(万件).当35≤x≤50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x之间的函数关系如图所示.乙种产品的销售单价在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
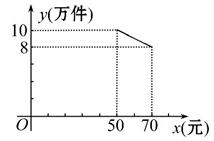
(1)当50≤x≤70时,求出甲种产品的年销售量y(万件)与x(元)之间的函数解析式.
(2)若该公司第一年的年销售利润(年销售利润=年销售收入-生产成本)为W(万元),那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?
(3)第二年公司可重新对产品进行定价,在(2)的条件下,并要求甲种产品的销售单价x(元)在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利(总盈利=两年的年销售利润之和-投资成本)不低于85万元.请求出第二年乙种产品的销售单价m(元)的范围.