正项数列｛
｝的前n项和为Sn，q为非零常数．已知对任意正整数n， m，当
时
总成立．
（1）求证：数列｛｝是等比数列；
（2）若互不相等的正整数n， m， k成等差数列，比较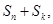
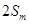的大小；
（3）（限理科生做，文科生不做）若正整数n， m， k成等差数列，求证：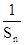
＋
≥
．
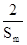相关试题
其最小值为
.
时，要使关于
的方程
有一个实根，求实数
的取值范围．
．
时，判断
在
的单调性，并用定义证明；
，不等式
恒成立，求
的取值范围；
（
）的最小正周期为
．
的单调增区间；
个单位，再向上平移
个单位，得到函数
的图像．求
上零点的个数．
，已知
，
．
的面积等于
，求
；
，求
.
，求
的值；
，求
的值．推荐套卷
正项数列｛｝的前n项和为Sn，q为非零常数．已知对任意正整数n， m，当时总成立．
（1）求证：数列｛｝是等比数列；
（2）若互不相等的正整数n， m， k成等差数列，比较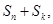 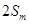的大小；
（3）（限理科生做，文科生不做）若正整数n， m， k成等差数列，求证：＋≥．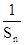
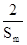粤公网安备 44130202000953号