某中学举行了“班班有歌声”活动,某校比赛聘请了10位老师和10位学生担任评委,其中甲班的得分情况如统计图(表)所示.
老师评分统计表格:
评委序号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
分数
|
94
|
96
|
93
|
91
|
X
|
92
|
91
|
98
|
96
|
93
|
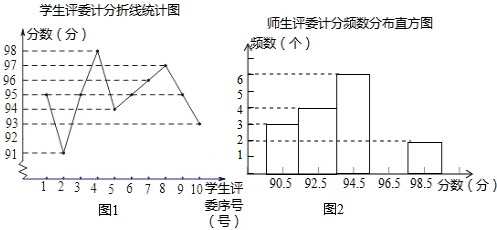
(1)在频数分布直方图中,自左向右第四组的频数为 ;
(2)学生评委计分的中位数是 分;
(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,并且按老师、学生各占60%、40%的方法计算各班最后得分.已知甲班最后得分为94.4分,求统计表中x的值.