把下列各数填在相应的表示集合的大括号内:
-2 ,π,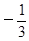 ,
,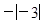 ,
,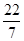 ,-0.3,1.7,
,-0.3,1.7,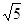 ,0 , 1.1010010001…(每两个1之间依次多一个0)
,0 , 1.1010010001…(每两个1之间依次多一个0)
整数{ ……}
负分数{ ……}
无理数{ ……}
相关知识点
推荐套卷
把下列各数填在相应的表示集合的大括号内:
-2 ,π,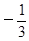 ,
,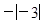 ,
,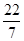 ,-0.3,1.7,
,-0.3,1.7,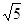 ,0 , 1.1010010001…(每两个1之间依次多一个0)
,0 , 1.1010010001…(每两个1之间依次多一个0)
整数{ ……}
负分数{ ……}
无理数{ ……}