在平面直角坐标系中,点 为坐标原点,抛物线 与 轴交于点 , ,与 轴交于点 ,顶点为 .
(1)求抛物线和直线 的解析式;
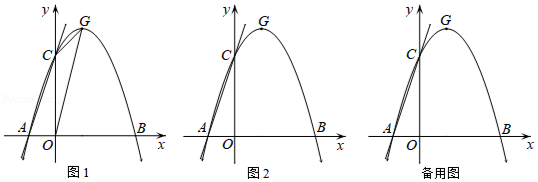
(2)如图1,设 为 轴上一动点,若 和 的面积满足 ,求点 的坐标;
(3)如图2,设点 从点 出发,以每秒1个单位长度的速度沿 轴向右运动,运动时间为 ,点 为射线 上一动点,过点 作 轴交抛物线对称轴右侧部分于点 .试探究点 在运动过程中,是否存在以 , , 为顶点的三角形为等腰直角三角形?若存在,求出 的值;若不存在,请说明理由.
相关知识点
推荐套卷


 ),解答下列问题:
),解答下列问题:

 粤公网安备 44130202000953号
粤公网安备 44130202000953号