已知,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度均为1cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).
(1)如图1,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
(2)如图2,当t为何值时,△PBQ是直角三角形?
(3)如图3,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,请直接写出∠CMQ度数.
相关知识点
推荐套卷
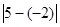 表示
表示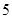 与
与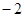 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为
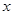 与
与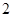 的两点之间的距离可以表示为__ ________.
的两点之间的距离可以表示为__ ________.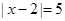 ,则
,则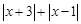 表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得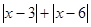 是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
是否有最小值?如果有,直接写出最小值;如果没有,说明理由.

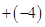 ,
,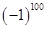 ,0,
,0, ,
,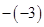

 ,
, 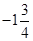 ,
, 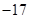 ,
, 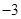 ,
,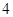 ,
, 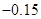 ,
, 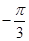 ,
, 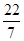 ,
, 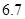 , 0.101001,
, 0.101001, 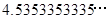 (每两个
(每两个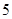 之间依次增加
之间依次增加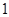 个
个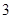 ).
).
 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号