已知圆M的圆心M在x轴上，半径为1，直线
：y=
x-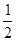
被圆M所截的弦长为
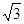，且圆心M在直线的下方．
（1）求圆M的方程；
（2）设A（0，t），B（0，t+6）（-5≤t≤-2），若圆M是△ABC的内切圆，求△ABC的面积S的最大值和最小值．
相关试题
，使
同时成立？若存在，求出
中，内角A，B，C的对边分别为
，已知
.
的值；
，求
函数
的定义域为R；命题
方程
有两个不相等的负数根，若
是假命题，求实数
的取值范围.
.
的单调区间；
，使
的解集；
的解集非空，求实数
的取值范围.相关知识点
推荐套卷
已知圆M的圆心M在x轴上，半径为1，直线：y=x-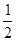被圆M所截的弦长为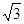，且圆心M在直线的下方．
（1）求圆M的方程；
（2）设A（0，t），B（0，t+6）（-5≤t≤-2），若圆M是△ABC的内切圆，求△ABC的面积S的最大值和最小值．
粤公网安备 44130202000953号