图，△ABC中，点E、P在边AB上，且AE＝BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3
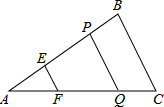
（1）求证：EF＋PQ＝BC
（2）若S1＋S3＝S2，求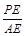
的值
相关知识点
推荐套卷
图，△ABC中，点E、P在边AB上，且AE＝BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3
（1）求证：EF＋PQ＝BC
（2）若S1＋S3＝S2，求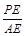的值
粤公网安备 44130202000953号