如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿CB方向平移得到的,连结AE,AC和BE相交于点O.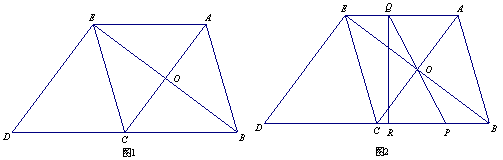
(1)判断四边形ABCE是怎样的四边形,并证明你的结论;
(2)如图2,P是线段BC上一动点(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,以点P、Q、R为顶点的三角形与△BOC相似?
相关知识点
推荐套卷
 ,反比例函数
,反比例函数 的图像经过点A,动直线
的图像经过点A,动直线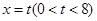 与反比例函数的图像交于点M,与直线AB交于点N.
与反比例函数的图像交于点M,与直线AB交于点N.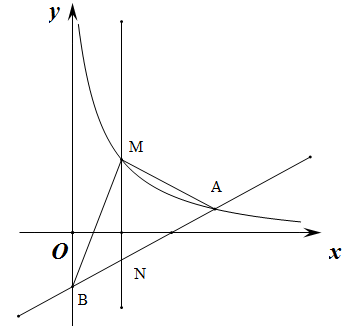
 ,求t的值.
,求t的值.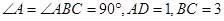 ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
 .
.
 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号