某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为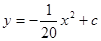 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)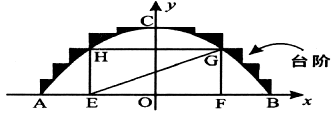
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
相关知识点
推荐套卷
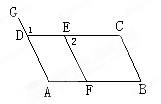
 (1)若∠A
(1)若∠A =∠1,则可判断_______∥_______,因为________.
=∠1,则可判断_______∥_______,因为________. ______.
______.
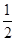 ,n=
,n=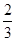
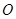 和
和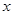 轴上另一点
轴上另一点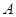 ,它的对称轴
,它的对称轴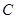 ,直线
,直线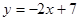 经过抛物线上一点
经过抛物线上一点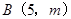 ,且与直线
,且与直线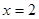 交于点
交于点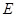 .
.
 的值及该抛物线的函数关系式;
的值及该抛物线的函数关系式;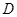 是
是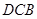 △∽△
△∽△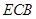 时,求点
时,求点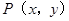 是该抛物线上的一个动点,是否存在这样的点
是该抛物线上的一个动点,是否存在这样的点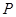 ,使得
,使得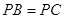 ,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号