将圆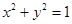
上每一点的横坐标都伸长为原来的
倍，纵坐标都伸长为原
来的2倍，得到曲线C．
（1）求曲线C的参数方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知点P的极坐标为
，且点P关于直线
的对称点为点Q，设直线PQ与曲线C相交于A、B两点，求线段AB的垂直平分线的极坐标方程．
的解集为
，求实数p与q的值．
，当y＜0时，有
，解关于x的不等式
B，试求k的取值范围．
在
上有最大值
，试确定常数
，并求这个函数在该闭区间上的最小值。推荐套卷
将圆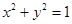上每一点的横坐标都伸长为原来的倍，纵坐标都伸长为原
来的2倍，得到曲线C．
（1）求曲线C的参数方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知点P的极坐标为，且点P关于直线的对称点为点Q，设直线PQ与曲线C相交于A、B两点，求线段AB的垂直平分线的极坐标方程．
粤公网安备 44130202000953号