已知定义域为 的二次函数的最小值为0,且有
的二次函数的最小值为0,且有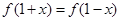 ,直线
,直线 的图象与
的图象与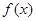 的图象交于两点,两点间的距离为
的图象交于两点,两点间的距离为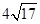 ,数列
,数列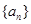 满足
满足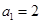
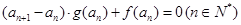 .
.
(1)求函数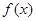 的解析式;
的解析式;
(2)求证数列 是等比数列;
是等比数列;
(3)设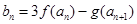 ,求数列{
,求数列{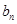 }的最小值及相应的
}的最小值及相应的
相关知识点
推荐套卷
已知定义域为 的二次函数的最小值为0,且有
的二次函数的最小值为0,且有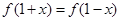 ,直线
,直线 的图象与
的图象与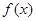 的图象交于两点,两点间的距离为
的图象交于两点,两点间的距离为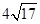 ,数列
,数列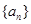 满足
满足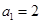
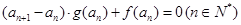 .
.
(1)求函数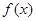 的解析式;
的解析式;
(2)求证数列 是等比数列;
是等比数列;
(3)设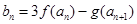 ,求数列{
,求数列{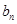 }的最小值及相应的
}的最小值及相应的