(理)已知动点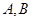 分别在
分别在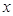 轴、
轴、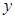 轴上,且满足
轴上,且满足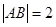 ,点
,点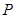 在线段
在线段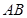 上,且
上,且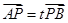
(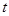 是不为零的常数)。设点
是不为零的常数)。设点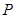 的轨迹为曲线
的轨迹为曲线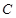 。
。
(1) 求点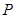 的轨迹方程;
的轨迹方程;
(2) 若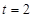 ,点
,点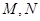 是
是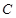 上关于原点对称的两个动点(
上关于原点对称的两个动点(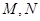 不在坐标轴上),点
不在坐标轴上),点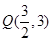 ,
,
(3) 求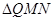 的面积
的面积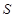 的最大值。
的最大值。
推荐套卷
(理)已知动点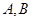 分别在
分别在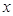 轴、
轴、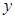 轴上,且满足
轴上,且满足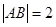 ,点
,点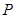 在线段
在线段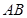 上,且
上,且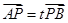
(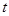 是不为零的常数)。设点
是不为零的常数)。设点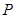 的轨迹为曲线
的轨迹为曲线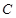 。
。
(1) 求点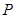 的轨迹方程;
的轨迹方程;
(2) 若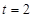 ,点
,点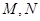 是
是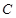 上关于原点对称的两个动点(
上关于原点对称的两个动点(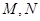 不在坐标轴上),点
不在坐标轴上),点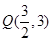 ,
,
(3) 求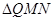 的面积
的面积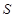 的最大值。
的最大值。