阅读材料：矩形的四个内角都是直角，矩形的对边平行且相等．利用阅读材料解决下列问题：如图，在矩形ABCD中，AB=6，BC=8，将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的F处．
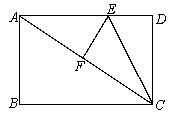
（1）求EF的长；
（2）求梯形ABCE的面积．
相关试题
看成了
，求得其结果为
，若
，请你帮助他求得正确答案．
与多项式
的和中，不含有
、
，求
,
，求A-2B的值
推荐套卷
阅读材料：矩形的四个内角都是直角，矩形的对边平行且相等．利用阅读材料解决下列问题：如图，在矩形ABCD中，AB=6，BC=8，将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的F处．
（1）求EF的长；
（2）求梯形ABCE的面积．
粤公网安备 44130202000953号