已知正方形ABCD中，AB＝BC＝CD＝AD=10cm，动点P，Q分别从点B，C同时出发沿正
方形的四周运动．设点P的运动速度为2cm/s，点Q的运动速度为3cm/s，设点P，Q运动的时间为t（s）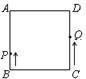
（1）若点P，Q作相向运动，且它们第一次相遇在AD边上，求t的值．
（2）在（1）中点P，Q第一次相遇后继续运动，到第2次相遇，第3次相遇，…，求第100次相遇时，
相遇地点在正方形ABCD哪条边上，请写出计算过程．
（3）若点P，Q作同向运动，求它们相遇时t的值．
相关试题
一个不透明的袋中，装有编号为①、②、③、④的四个球，它们除了编号外其余都相同．
（1）从袋中任意摸出一个球，摸到编号为奇数的球的概率为 ；
（2）从袋中任意摸出两个球，求摸到的球编号都为奇数的概率．
某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
根据以上信息完成下列问题：
（1）统计表中的m= ，n= ，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是 ；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
）÷
．
-π）0+|1-
．
与x轴交于点A、B两点，与y轴交于点C，且A点坐标（-3，0），连接BC、AC．
相关知识点
推荐套卷
粤公网安备 44130202000953号