海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为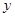 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里 处,如图.现假设:
处,如图.现假设: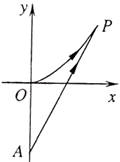
①失事船的移动路径可视为抛物线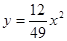 ;
;
②定位后救援船即刻沿直线匀速前往救援;
③救援船出发 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为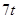 .
.
(1)当 时,写出失事船所在位置
时,写出失事船所在位置 的纵坐标.若此时两船恰好会合,求救援船速度的大小;
的纵坐标.若此时两船恰好会合,求救援船速度的大小;
(2)问救援船的时速至少是多少海里才能追上失事船?
相关知识点
推荐套卷
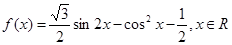
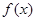 的最小正周期;
的最小正周期;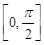 上的单调性并求在此区间上
上的单调性并求在此区间上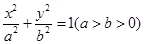 经过点
经过点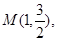 离心率为
离心率为 。
。 ,
, 的单调区间和极值点;
的单调区间和极值点;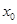 ,记过点
,记过点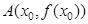 与原点的直线斜率为
与原点的直线斜率为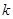 。是否存在
。是否存在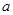 使
使 ?若存在,求出
?若存在,求出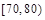
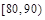
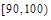
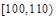
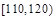
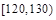
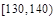
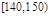
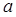
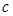
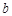
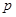 ;
;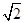 ,F是BC的中点.
,F是BC的中点.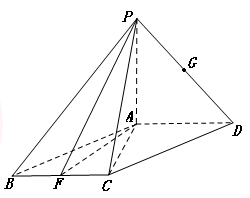
 粤公网安备 44130202000953号
粤公网安备 44130202000953号