在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: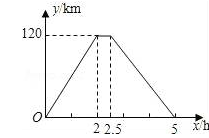
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中y与x之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
相关知识点
推荐套卷
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中y与x之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.