某卖场同时销售变频冷暖空调机和智能洗衣机，这两种产品的市场需求量大，有多少卖多少。今年元旦假期7天该卖场要根据实际情况确定产品的进货数量，以达到总利润最大。已知两种产品直接受资金和劳动力的限制。根据过去销售情况，得到两种产品的有关数据如下表：（表中单位：百元）
试问：怎样确定两种货物的进货量，才能使7天的总利润最大，最大利润是多少？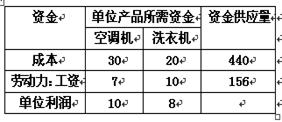
相关试题
，
，
不能为同一等差数列中的三项．
Sn(n＝1，2，3，…)，证明：
是等比数列；
满足a1＝0且
－
＝ 1.
，记Sn＝
，证明：Sn<1.
≤bn＋1(n∈N*)；②bn≤M(n∈N*，M是与n无关的常数)的无穷数列{bn}叫“特界” 数列．推荐套卷
某卖场同时销售变频冷暖空调机和智能洗衣机，这两种产品的市场需求量大，有多少卖多少。今年元旦假期7天该卖场要根据实际情况确定产品的进货数量，以达到总利润最大。已知两种产品直接受资金和劳动力的限制。根据过去销售情况，得到两种产品的有关数据如下表：（表中单位：百元）
试问：怎样确定两种货物的进货量，才能使7天的总利润最大，最大利润是多少？
粤公网安备 44130202000953号