已知椭圆C：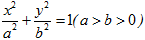
的离心率与等轴双曲线的离心率互为倒数关系，直线
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切．
（1）求椭圆C的方程；
（2）设M是椭圆的上顶点，过点M分别作直线MA、MB交椭圆于A、B两点，设两直线的斜率分别为k1、k2，且k1+k2=4，证明：直线AB过定点（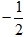
，-l）．
相关试题
在点
和
处的切线方程。
与
,当
时,平均增长率的大小.
、
、
是同一平面内三条不重合自上而下的平行直线．
的三顶点分别放在
和
，
，求
的范围？
推荐套卷
已知椭圆C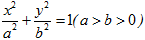：的离心率与等轴双曲线的离心率互为倒数关系，直线与以原点为圆心，以椭圆C的短半轴长为半径的圆相切．
（1）求椭圆C的方程；
（2）设M是椭圆的上顶点，过点M分别作直线MA、MB交椭圆于A、B两点，设两直线的斜率分别为k1、k2，且k1+k2=4，证明：直线AB过定点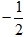（，-l）．
粤公网安备 44130202000953号