图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.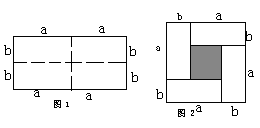

(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(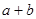 )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含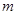 、
、 的代数式表示).
的代数式表示).
相关知识点
推荐套卷
图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.

(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(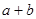 )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含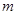 、
、 的代数式表示).
的代数式表示).