( 本小题12分) 某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案.抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽”卡的概率是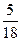 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)在(I)下,甲乙丙丁四人依次抽奖,至少有两人获奖的概率.