以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位已知直线 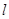 的参数方程为
的参数方程为 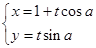 (t为参数,
(t为参数,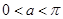 ),曲线C的极坐标方程为
),曲线C的极坐标方程为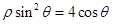
(Ⅰ)求曲线C的直角坐标方程。
(Ⅱ)设直线 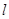 与曲线C相交于A,B两点,当
与曲线C相交于A,B两点,当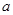 变化时,求
变化时,求 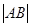 的最小值
的最小值
推荐套卷
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位已知直线 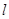 的参数方程为
的参数方程为 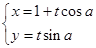 (t为参数,
(t为参数,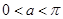 ),曲线C的极坐标方程为
),曲线C的极坐标方程为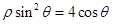
(Ⅰ)求曲线C的直角坐标方程。
(Ⅱ)设直线 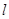 与曲线C相交于A,B两点,当
与曲线C相交于A,B两点,当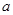 变化时,求
变化时,求 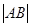 的最小值
的最小值