在网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=6．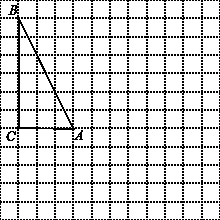
（1）试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB′C′；
（2）若点B的坐标为（-4，5），试建立合适的直角坐标系，并写出A、C两点的坐标；
（3）作出与△ABC关于原点对称的图形△A″B″C″，并写出A″、B″、C″三点的坐标．
，求另一数；
×
÷（－16）
）÷（－5）×（－3
）
）÷（－9）
）÷（－15）相关知识点
推荐套卷
在网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=6．
（1）试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB′C′；
（2）若点B的坐标为（-4，5），试建立合适的直角坐标系，并写出A、C两点的坐标；
（3）作出与△ABC关于原点对称的图形△A″B″C″，并写出A″、B″、C″三点的坐标．
粤公网安备 44130202000953号