如图1，抛物线
经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B．
（1）求抛物线和直线BC的解析式；
（2）如图2，点P为第一象限抛物线上一点，是否存在使△PBC面积最大的点P？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与直线BC相交于点F，M为直线BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．
（本小题满分10分）如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连结CP，过点P作PM⊥CP交AB于点D，且PM＝CP，过点M作MN∥OA，交BO于点N，连结ND、BM，设OP＝
．
（1）求点M的坐标（用含的代数式表示）；
（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由；
（3）当为何值时，四边形BNDM的面积最小．
（本小题满分10分）如图，顶点M在
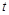轴上的抛物线与直线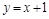
相交于A、B两点，且点A在
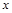轴上，点B的横坐标为2，连结AM、BM．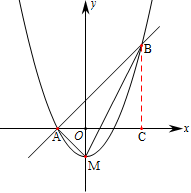
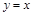（1）求抛物线的函数关系式；
（2）判断△ABM的形状，并说明理由；
（3）把抛物线与直线
的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（
，
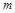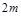），当满足什么条件时，平移后的抛物线总有不动点？
（本小题满分8分）如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E．
（1）求证：CE为⊙O的切线；
（2）判断四边形AOCD是否为菱形？并说明理由．
（本小题满分8分）某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体实验．测得成人服药后血液中药物深度
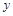（微克/毫升）与服药时间
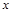小时之间的函数关系如图所示（当
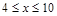时，与成反比）．
（1）根据图象分别求出血液中药物浓度上升和下降阶段与之间的函数关系式；
（2）问血液中药物浓度不低于4微克/毫升的持续时间为多少小时？
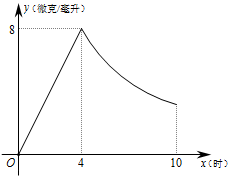
粤公网安备 44130202000953号