一家化工厂原来每月利润为120万元,从今年1月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平.
(1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y,写出y关于x的函数关系式,并求前几个月的利润和等于700万元;
(2)当x为何值时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等;
(3)求使用回收净化设备后两年的利润总和.
相关知识点
推荐套卷
 ﹣
﹣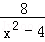 .
. 时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y="5" 即2(2x+5y)+y=5③
时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y="5" 即2(2x+5y)+y=5③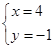 .
. ;
; .
. 的值;
的值; 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号