如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC=EB，AB=4，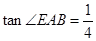
．
（Ⅰ）证明：平面ADE⊥平面ACD；
（Ⅱ）当三棱锥C-ADE体积最大时，求二面角D-AE-B的余弦值．
中，角
、
、
对的边分别为
、
、
，且
，
.
的值；
，求
.
，
，
的解析式，并求它的单调递增区间；
有四个不相等的实数根，求
的取值范围。
。
的最小正周期和单调递增区间；
上的最小值和最大值，并求出取最值时
的值。
，求它的定义域和值域。
，计算：
；
．相关知识点
推荐套卷
如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC=EB，AB=4，．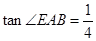
（Ⅰ）证明：平面ADE⊥平面ACD；
（Ⅱ）当三棱锥C-ADE体积最大时，求二面角D-AE-B的余弦值．
粤公网安备 44130202000953号