已知 是最大的负整数,b是多项式
是最大的负整数,b是多项式 的次数,c是单项式
的次数,c是单项式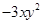 的系数,且
的系数,且 、b、c分别是点A、B、C在数轴上对应的数.
、b、c分别是点A、B、C在数轴上对应的数.
(1)求 、b、c的值,并在数轴上标出点A、B、C.
、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒1个单位长度,点Q的速度是每秒 个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请直接写出所有点M对应的数.(不必说明理由).
相关知识点
推荐套卷
已知 是最大的负整数,b是多项式
是最大的负整数,b是多项式 的次数,c是单项式
的次数,c是单项式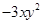 的系数,且
的系数,且 、b、c分别是点A、B、C在数轴上对应的数.
、b、c分别是点A、B、C在数轴上对应的数.
(1)求 、b、c的值,并在数轴上标出点A、B、C.
、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒1个单位长度,点Q的速度是每秒 个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请直接写出所有点M对应的数.(不必说明理由).