如图, 为一直角三角形草坪,其中
为一直角三角形草坪,其中 ,
, 米,
米, 米,为了重建草坪,设计师准备了两套方案:
米,为了重建草坪,设计师准备了两套方案:
方案一:扩大为一个直角三角形,其中斜边 过点
过点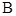 ,且与
,且与 平行,
平行, 过点
过点 ,
, 过点
过点 ;
;
方案二:扩大为一个等边三角形,其中 过点
过点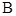 ,
, 过点
过点 ,
, 过点
过点 .
.
(1)求方案一中三角形 面积
面积 的最小值;
的最小值;
(2)求方案二中三角形 面积
面积 的最大值.
的最大值.
推荐套卷
如图, 为一直角三角形草坪,其中
为一直角三角形草坪,其中 ,
, 米,
米, 米,为了重建草坪,设计师准备了两套方案:
米,为了重建草坪,设计师准备了两套方案:
方案一:扩大为一个直角三角形,其中斜边 过点
过点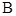 ,且与
,且与 平行,
平行, 过点
过点 ,
, 过点
过点 ;
;
方案二:扩大为一个等边三角形,其中 过点
过点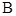 ,
, 过点
过点 ,
, 过点
过点 .
.
(1)求方案一中三角形 面积
面积 的最小值;
的最小值;
(2)求方案二中三角形 面积
面积 的最大值.
的最大值.