已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)
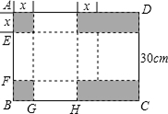
(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积
相关知识点
推荐套卷
已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)

(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积