如图，在边长均为1的小正方形网格纸中，△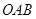
的顶点
、
、
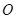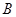均在格点上，且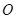是直角坐标系的原点，点在
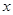轴上．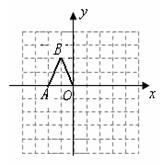
（1）以O为位似中心，将△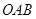放大，使得放大后的△
与△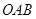对应线段的比为2∶1，画出△ ．（所画△与△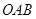在原点两侧）．
（2）求出线段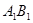
所在直线的函数关系式．
相关试题
，判断直线BC与ED的位置关系并请说明理由．
．
，求出∠BOD的的度数；
，其中
．相关知识点
推荐套卷
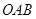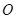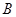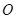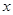如图，在边长均为1的小正方形网格纸中，△的顶点、、均在格点上，且是直角坐标系的原点，点在轴上．
（1）以O为位似中心，将△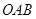放大，使得放大后的△与△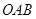对应线段的比为2∶1，画出△ ．（所画△与△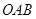在原点两侧）．
（2）求出线段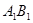所在直线的函数关系式．
粤公网安备 44130202000953号