某校园商店经销甲、乙两种文具.现有如下信息:

请根据以上信息,解答下列问题:
(1)甲、乙两种文具的零售单价分别为 元和 元.(直接写出答案)
(2)该校园商店平均每天卖出甲文具50件和乙文具120件.经调查发现,甲种文具零售单价每降0.1元,甲种文具每天可多销售10件.为了降价促销,使学生得到实惠,商店决定把甲种文具的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,可以使商店每天销售甲、乙两种文具获取的利润保持不变?
相关知识点
推荐套卷
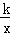 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).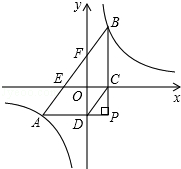
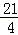 时,求点P的坐标.
时,求点P的坐标.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号