如图，△ABC中，AB=AC=2，∠B=∠C=40°．点D在线段BC上运动（点D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
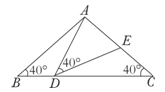
（1）当∠BAD=20°时，∠EDC= °；
（2）当DC等于多少时，△ABD≌△DCE，试说明理由；
（3）△ADE能成为等腰三角形吗？若能，请直接写出此时∠BAD的度数；若不能，请说明理由．
相关试题
．
的值．
．
个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动，经过点M的直线l⊥x轴，交AC或BC于点P，设点M的运动时间为t秒（t>0），求点M的运动时间t与△APH的面积S的函数关系式，并求出S的最大值。相关知识点
推荐套卷
如图，△ABC中，AB=AC=2，∠B=∠C=40°．点D在线段BC上运动（点D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
（1）当∠BAD=20°时，∠EDC= °；
（2）当DC等于多少时，△ABD≌△DCE，试说明理由；
（3）△ADE能成为等腰三角形吗？若能，请直接写出此时∠BAD的度数；若不能，请说明理由．
粤公网安备 44130202000953号