已知函数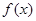 是定义在
是定义在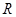 上的奇函数,当
上的奇函数,当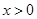 时,
时,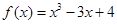 .
.
(1)求函数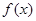 的解析式;
的解析式;
(2)①证明函数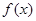 在
在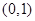 上是单调递减函数;
上是单调递减函数;
②判断函数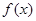 在
在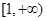 上的单调性(不要证明);
上的单调性(不要证明);
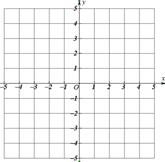
(3)根据你对该函数的理解,作出函数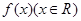 的图像.(不需要说明理由,但要有关键特征,标出关键点)
的图像.(不需要说明理由,但要有关键特征,标出关键点)
(本题可能使用到的公式: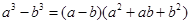 )
)
相关知识点
推荐套卷
已知函数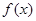 是定义在
是定义在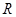 上的奇函数,当
上的奇函数,当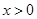 时,
时,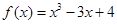 .
.
(1)求函数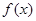 的解析式;
的解析式;
(2)①证明函数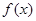 在
在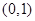 上是单调递减函数;
上是单调递减函数;
②判断函数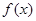 在
在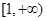 上的单调性(不要证明);
上的单调性(不要证明);
(3)根据你对该函数的理解,作出函数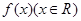 的图像.(不需要说明理由,但要有关键特征,标出关键点)
的图像.(不需要说明理由,但要有关键特征,标出关键点)
(本题可能使用到的公式: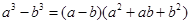 )
)