(1)一个两位数,十位上的数字为a,个位上的数字为b,把这个两位数的十位上的数字与个数上的数字对调后得到一个新的两位数。新的两位数与原来的两位数之和是11的倍数吗?说说你的理由。
(2)任意写一个三位数(个位上的数字不为零),把这个三位数的百位上的数字与个位上的数字对调后得到一个新的三位数(三位数的十位上的数字保持不变),如果把这两个三位数中的较大的三位数减去较小的三位数,那么请你猜一猜这两个三位数之差一定是哪几个数的倍数(1的倍数除外)?说说你的理由。
相关知识点
推荐套卷
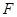 从点
从点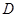 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿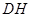 运动到点
运动到点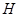 停止,在运动过程中,过点
停止,在运动过程中,过点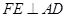 交折线
交折线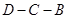 于点
于点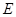 ,将纸片沿直线
,将纸片沿直线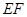 折叠,点
折叠,点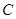 、
、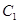 、
、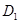 。设
。设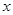 秒(
秒(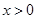 )。
)。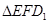 或四边形
或四边形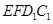 与梯形
与梯形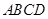 重叠部分面积为
重叠部分面积为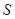 ,请直接写出
,请直接写出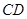 ,交线段
,交线段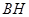 于点
于点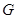 ,交线段
,交线段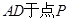 。在直线
。在直线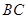 上存在点
上存在点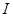 ,使
,使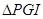 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段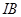 的所有可能的长度。
的所有可能的长度。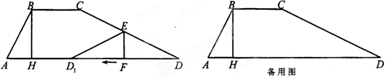
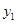 (台)
(台)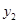 (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势: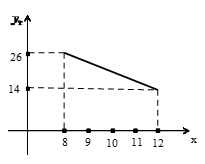
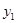 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式;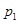 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: 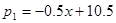 ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入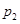 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: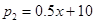 (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号