(本题6分)有理数a,b,c在数轴上的位置如图所示,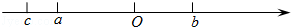
(1)c__________0; b+c__________0;b-a__________0(用“>、<、=”填空)
(2)试化简:|b-a |-| b+c |+|c|.
相关知识点
推荐套卷
(本题6分)有理数a,b,c在数轴上的位置如图所示,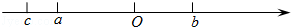
(1)c__________0; b+c__________0;b-a__________0(用“>、<、=”填空)
(2)试化简:|b-a |-| b+c |+|c|.