（年蒙自市初中学业水平第一次模拟测试）在某市地铁施工期间，交管部门在施工路段设立了矩形路况警示牌（如图所示）．已知立杆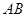
的高度是
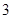米，从路侧点
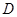处测得路况警示牌顶端
点和底端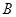
点的仰角分别是
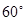和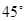
，求路况警示牌宽
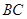的值．（精确到0．1米）（参考数据：
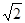≈1．41，
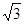≈1．73）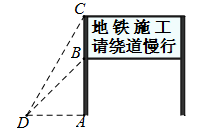
，求
的值
比－
的值大1？
相关知识点
推荐套卷
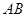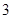（年蒙自市初中学业水平第一次模拟测试）在某市地铁施工期间，交管部门在施工路段设立了矩形路况警示牌（如图所示）．已知立杆的高度是米，从路侧点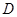处测得路况警示牌顶端点和底端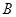点的仰角分别是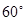和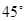，求路况警示牌宽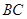的值．（精确到0．1米）（参考数据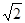：≈1．41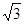，≈1．73）
粤公网安备 44130202000953号