如图，平行四边形ABCD中，AB=3cm,BC=5cm,∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
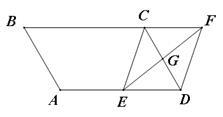
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）
如图，平行四边形ABCD中，AB=3cm,BC=5cm,∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）
，
，
，
．
，
，
．
与
；
与
．
．
粤公网安备 44130202000953号