(黔西南州)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为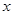 吨,应交水费为
吨,应交水费为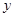 元,写出
元,写出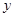 与
与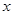 之间的函数关系式;
之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
(黔西南州)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为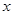 吨,应交水费为
吨,应交水费为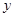 元,写出
元,写出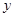 与
与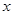 之间的函数关系式;
之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?