（百色）已知⊙O为△ABC的外接圆，圆心O在AB上．
（1）在图1中，用尺规作图作∠BAC的平分线AD交⊙O于D（保留作图痕迹，不写作法与证明）；
（2）如图2，设∠BAC的平分线AD交BC于E，⊙O半径为5，AC=4，连接OD交BC于F．
①求证：OD⊥BC；
②求EF的长．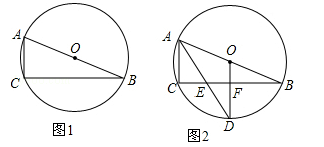
（百色）已知⊙O为△ABC的外接圆，圆心O在AB上．
（1）在图1中，用尺规作图作∠BAC的平分线AD交⊙O于D（保留作图痕迹，不写作法与证明）；
（2）如图2，设∠BAC的平分线AD交BC于E，⊙O半径为5，AC=4，连接OD交BC于F．
①求证：OD⊥BC；
②求EF的长．
的值与x的值无关，求m的值．
；
．
的意义是
．
．
的值．
时，
值．
粤公网安备 44130202000953号