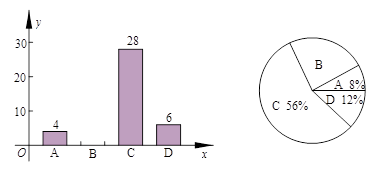随着社会经济的发展,汽车逐渐走入平常百姓家.某数学兴趣小组随机抽取了我市某单位部分职工进行调查,对职工购车情况分4类(A:车价40万元以上;B:车价在20—40万元;C:车价在20万元以下;D:暂时未购车)进行了统计,并将统计结果绘制成以下条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)调查样本人数为__________,样本中B类人数百分比是_______,其所在扇形统计图中的圆心角度数是________;
(2)把条形统计图补充完整;
(3)该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.