如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<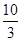 ),连接MN.
),连接MN.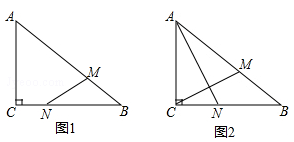
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<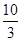 ),连接MN.
),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.