如图,过原点的直线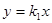 和
和 与反比例函数
与反比例函数 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.

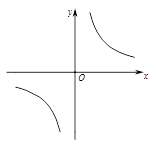
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时 和
和 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(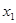 ,
, ),Q(
),Q( ,
, )(
)(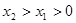 )是函数
)是函数 图象上的任意两点,
图象上的任意两点, ,
, ,试判断
,试判断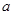 ,
, 的大小关系,并说明理由.
的大小关系,并说明理由.
如图,过原点的直线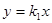 和
和 与反比例函数
与反比例函数 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.


(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时 和
和 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(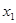 ,
, ),Q(
),Q( ,
, )(
)(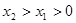 )是函数
)是函数 图象上的任意两点,
图象上的任意两点, ,
, ,试判断
,试判断 ,
, 的大小关系,并说明理由.
的大小关系,并说明理由.