如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动。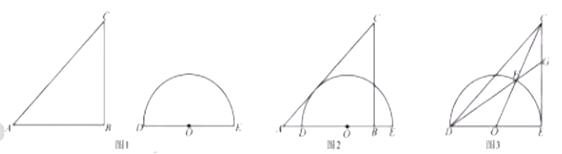
(1)当B与O重合的时候,求三角板运动的时间;
(2)如图2,当AC与半圆相切时,求AD;
(3)如图3,当AB和DE重合时,求证: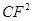 =CG·CE.
=CG·CE.
如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动。
(1)当B与O重合的时候,求三角板运动的时间;
(2)如图2,当AC与半圆相切时,求AD;
(3)如图3,当AB和DE重合时,求证: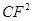 =CG·CE.
=CG·CE.