在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同．
（1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；
（2）现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是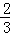
，请求出后来放入袋中的红球的个数．
在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同．
（1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；
（2）现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是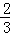，请求出后来放入袋中的红球的个数．
轴对称的△A1B1C1，写出△ABC关于
轴对称的△A2B2C2的各点坐标.
，再从1、0、-1三个数中，选择一个你认为合适的数作为
的值代入求值。
粤公网安备 44130202000953号