在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有有无数多个.
(1)若点M(2,a)是反比例函数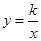 (k为常数,
(k为常数,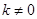 )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;
(2)函数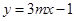 (m为常数,
(m为常数,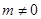 )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有有无数多个.
(1)若点M(2,a)是反比例函数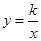 (k为常数,
(k为常数,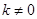 )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;
(2)函数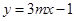 (m为常数,
(m为常数,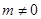 )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.