为了倡导“节约用水,从我做起”,宜兴市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.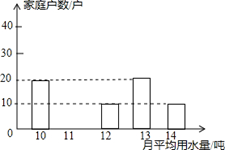
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计宜兴市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
相关知识点
推荐套卷
为了倡导“节约用水,从我做起”,宜兴市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计宜兴市直机关500户家庭中月平均用水量不超过12吨的约有多少户?